
집합 A의 크기를 |A|라고 하며, 이를 A의 크기 혹은 카디널리티(cardinality)라고 부른다. 이 개념은 집합이 몇 개의 원소를 가지고 있는지를 나타낸다. 집합의 크기는 크게 두 가지로 나뉜다: 유한 집합과 무한 집합이다.
유한 집합과 무한 집합
집합은 유한 집합(finite set)과 무한 집합(infinite set)으로 구분할 수 있다.
유한 집합 (Finite Set)
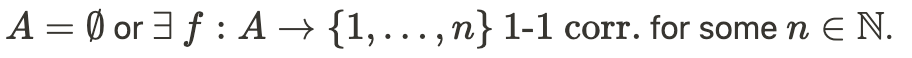
- 집합 A가 공집합인 경우, 즉 A가 아무 원소도 포함하지 않는 경우, A는 유한 집합이다. 이때, A의 크기를 0이라고 정의하며, 이를 |A| = 0이라고 쓴다.
- 만약 집합 A의 원소들이 어떤 자연수 집합 {1, 2, …, n}과 1-1 대응(일대일 대응, 1-1 correspondence)을 가질 수 있는 경우, 이 집합 A는 유한 집합이다. 이때 A의 크기는 n이라고 정의하며, 이를 |A| = n이라고 쓴다. 여기서 n은 자연수이다.
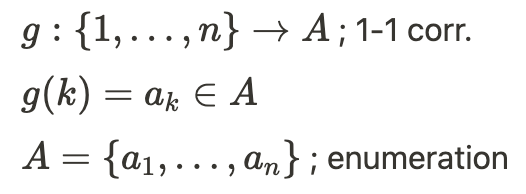
예를 들어, 함수 g가 {1, 2, …, n}에서 집합 A로 가는 1-1 대응 함수라면, 각 자연수 k에 대해 g(k)를 A의 원소 a_k로 정의할 수 있다. 이렇게 정의된 A는 A = {a_1, a_2, …, a_n}과 같이 나열할 수 있으며, 이를 열거(enumeration)라고 한다. 따라서, 유한 집합은 그 원소들을 나열할 수 있으며, 이 경우 그 집합의 크기는 그 원소의 개수와 같다.
무한 집합: 가산(countable)과 비가산(uncountable)
무한 집합은 다시 가산 집합(countable set)과 비가산 집합(uncountable set)으로 나눌 수 있다.
a. 가산 무한 집합 (Countably Infinite Set)
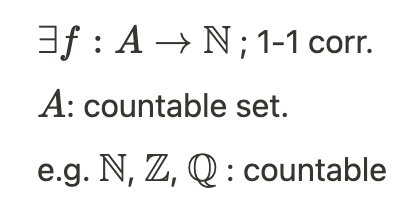
집합 A가 자연수 집합(예: {1, 2, 3, ...})과 1-1 대응할 수 있는 경우, A는 가산 무한 집합이다. 이때 자연수 집합은 N 전체를 의미하며, 이는 유한 집합에서의 자연수 집합 {1, 2, ..., n}과 다르다. 유한 집합에서는 n이 집합의 크기를 나타내는 고정된 숫자이지만, 가산 무한 집합에서는 자연수 전체를 사용하여 대응이 이루어지기 때문에 n이라는 유한한 수가 존재하지 않는다.
가산 집합의 예로는 자연수 집합(N), 정수 집합(Z), 그리고 유리수 집합(Q)이 있다.
정수 집합 Z가 가산 집합이라는 사실은 다음과 같이 증명할 수 있다.

예를 들어,
a0 = 0
a1 = -1
a2 = 1
a3 = -2
a4 = 2
a5 = -3
a6 = 3
이렇게 진행된다고 할때 f(n)은 다음과 같이 정의할 수 있다.
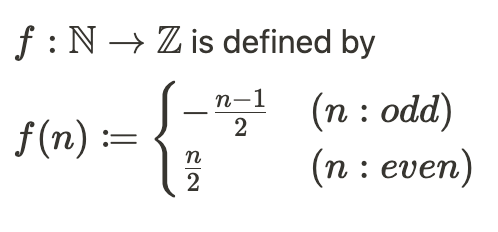
함수 f를 정의하는데, n이 홀수일 때 (-n+1)/2로, n이 짝수일 때 n/2로 정의한다. 이 정의에 따르면, 자연수 집합 N과 정수 집합 Z 사이에 1-1 대응이 성립하므로, 정수 집합 Z는 가산 집합이다.

위 표현은 집합 A가 원소들을 나열할 수 있다는 것을 의미한다. 즉, A의 원소들을 순서대로 a1, a2, ...와 같이 나열할 수 있을 때, 이를 열거(enumeration)라고 부른다. 이 경우, 집합 A는 유한 집합이거나 가산 무한 집합일 수 있다. 가산 무한 집합의 경우, 집합의 원소들이 자연수 집합 N과 1-1 대응할 수 있음을 의미한다.
A : at most countable if A is finite or countably infinite.
이 문장은 집합 A가 유한 집합이거나 가산 무한 집합일 경우, “at most countable”(최대 가산 집합)이라고 부른다는 것을 의미한다. 즉, A가 유한한 경우에는 당연히 가산이며, A가 가산 무한 집합일 때도 자연수 집합과 1-1 대응할 수 있기 때문에 “at most countable”이다. “at most countable”라는 용어는 집합이 유한하거나 가산 무한임을 포함하는 표현이다.
b. 비가산 무한 집합 (Uncountable Set)

- 집합 A가 무한 집합이지만, 자연수 집합과 1-1 대응할 수 없다면, A는 비가산 무한 집합이다. 이러한 집합을 비가산 집합이라고 부른다.
- 예를 들어, 실수 집합 R은 비가산 집합이다. 이는 칸토어의 대각선 논법(Cantor’s diagonal argument)을 통해 증명할 수 있다. 이 증명에서는, 임의의 실수 집합이 자연수 집합과 1-1 대응할 수 없음을 보이며, 따라서 실수 집합은 가산 무한 집합이 아니라는 결론에 이른다.
- 이로 인해 실수 집합 R을 {x_1, x_2, …}와 같이 나열할 수 없으며, 이는 실수 집합 R이 가산 집합이 아님을 나타낸다.
정리하면, 집합의 크기는 유한 집합인지 무한 집합인지에 따라 나뉘며, 무한 집합일 경우 다시 가산 무한 집합과 비가산 무한 집합으로 나눌 수 있다. 이러한 구분은 집합의 원소들을 어떻게 대응시킬 수 있는지, 그리고 그 크기가 어떻게 정의되는지에 따라 달라진다.
'Upstage AI Lab 4기' 카테고리의 다른 글
| [Upstage AI Lab 4기] '아파트 실거래가 예측' 경진대회 Private Rank 3등 후기 (1) | 2024.09.17 |
|---|---|
| 가설 검정 - 유의수준, 검정통계량, 임계값, 기각역 (0) | 2024.08.23 |
| [팀프로젝트] 페르소나를 이용한 오은영 박사님 챗봇 (2) - chat history와 주제와 관계 없는 질문 회피 (1) | 2024.08.19 |
| [팀프로젝트] 페르소나를 이용한 오은영 박사님 챗봇 (1) 데이터 수집 및 임베딩, 쿼리 테스트 (0) | 2024.08.13 |
| [송인서 강사님] AI Engineer로의 첫걸음 + OT 후기 (1) | 2024.07.16 |
