
가설 검정
가설 검정은 통계적으로 어떤 주장(귀무가설)이 사실인지 확인하는 방법이다. 이 과정에서 우리는 두 가지 가설을 세 운다:
- 귀무가설 (H_0): 보통 우리가 검정하고자 하는 기본 가정. (마음속으로는 기각하고자 하는 가정)
- 대립가설 ((H_1)): 귀무가설이 사실이 아닐 경우를 나타내는 가설. (마음속으로는 채택하고 싶은 가정)
유의수준 (α)과 1종 오류
유의수준(α)은 가설 검정에서 귀무가설을 잘못 기각할 확률을 나타낸다. 이 값은 우리가 허용하는 1종 오류의 최대 확률이다. 1종 오류는 귀무가설이 사실임에도 불구하고 이를 기각하는 오류를 의미한다. 일반적으로 유의수준은 0.05(5%)로 설정되며, 이는 “귀무가설이 사실일 때 5%의 확률로 잘못된 결정(귀무가설 기각)을 내릴 수 있다”는 뜻 이다.

이때 유의수준이 중요한 이유는, 가설 검정의 목표가 대립가설을 검증하기 위함이라는 점에 있다. 즉, 귀무가설을 기각하고 대립가설을 채택하고자 하는 경향이 있으므로, 이 과정에서 발생할 수 있는 오류(1종 오류)를 가능한 한 최소화하고자 유의수준을 설정하는 것이다.
z-값 (z-score): 검정통계량
검정통계량(Test Statistic)은 가설 검정에서 우리가 어떤 결정을 내릴 때 사용하는 중요한 도구이다. 이를 통해 우리가 얻은 표본 데이터를 바탕으로 귀무가설을 기각할지 아니면 유지할지를 판단할 수 있다.
검정통계량은 주어진 표본 데이터를 바탕으로 계산된 통계량으로, 가설 검정에서 사용된다. 이를 통해 주어진 표본이 귀무가설 하에서 얼마나 벗어나 있는지를 평가할 수 있다. 검정통계량의 종류는 여러 가지가 있으며, 그 중 하나가 z-값이다.
z-값은 검정통계량 중 하나로, 주어진 데이터가 귀무가설 하에서 얼마나 벗어나 있는지를 측정하는 값이다. 이는 표본 평균이 귀무가설에서 가정된 모평균으로부터 몇 개의 표준 편차만큼 떨어져 있는지를 나타낸다. z-값이 크다면, 표본 평균이 귀무가설 하의 모평균으로부터 많이 떨어져 있다는 의미이며, 이 경우 귀무가설을 기각할 가능성이 크다. 반대로 z-값이 작다면, 표본 평균이 귀무가설 하의 모평균에 가깝다는 의미이며, 귀무가설을 기각하지 않을 가능성이 크다.
z-값은 다음과 같은 식으로 계산된다:
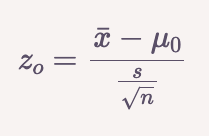
- bar(x): 표본 평균
- mu_0: 귀무가설 하에서의 모평균(가정된 평균)
- s: 표본 표준편차
- n: 표본 크기
즉, 검정통계량으로서 z-값을 사용하여, 우리가 얻은 표본이 귀무가설에서 가정된 평균으로부터 얼마나 벗어나 있는지를 평가하고, 이를 바탕으로 귀무가설을 기각할지 유지할지를 결정하는 것이다.
임계값과 기각역
- 기각역: 유의수준에 따라 검정통계량이 귀무가설을 기각할 수 있는 영역을 기각역이라고 한다. α = 0.05인 경우, 양측 검정에서는 기각역이 표준 정규 분포의 양쪽 끝 각각 2.5%씩에 해당한다. 이 기각역을 구체적으로 결정하기 위해 임계값(critical value)을 사용한다.
- 임계값: 임계값은 표준 정규 분포에서 유의수준에 대응하는 z-값이다. α = 0.05의 경우, 임계값은 ±1.96으로 설정된다. 즉, z-값이 1.96보다 크거나 -1.96보다 작다면, 이는 기각역에 속하게 되며 귀무가설을 기각할 수 있다.
예시로 보는 가설검정
예시는 단일 표본 t-test이다.
어느 제과 회사에서 나오는 쿠키의 평균 무게가 50g인지 확인하기 위해 30개의 샘플을 조사했다. 이 샘플들의 평균 무게는 52g이었고, 표준편차는 4g이었다. 이 정보를 바탕으로 z-값을 계산해 보니, 2.74가 나왔다.
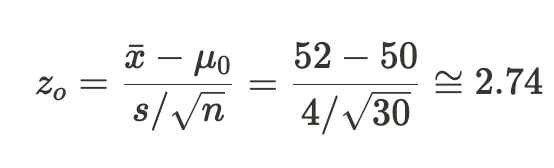
이제, 이 z-값을 임계값과 비교해보자. α = 0.05일 때, 임계값은 ±1.96이다. 계산된 z-값 2.74는 1.96을 초과하므로, 이 값은 기각역에 속한다.
즉, "쿠키의 평균 무게는 50g이다" 라는 귀무가설을 기각하고 "쿠키의 평균 무게는 50g이 아니다" 라는 대립가설을 채택하지 않을 이유가 없음을 보였다.
'대립가설을 채택했다.' 하고 하면 그냥 채택된것으로 끝난다.
'채택하지 않을 이유가 없음을 보였다.' 라는건 이건 빼박이다. 라는 소리다. 무조건 채택 해야해. 라는 뉘앙스다.
지금은 연습문제니까 그냥 '저 이거 채택했는데요?'라고 할 수 있지만 어디 학회에서 발표를 할때 근거를 얘기할때 '채택했다.' 이렇게 말하면 '너 대립가설 기각할수도 있었자나' 이런 반박이 안나올 수 있다. 이때, '채택하지 않을 이유가 없어. 라고 말하면 좋다. 꼭 채택해야만 했었어. 라는 뉘앙스로 전달하는게 좋다.
이게 위에서 언급한 '귀무가설은 기각하고 싶고, 대립가설을 채택하고싶다'는 마인드가 반영이 된거다.
그리고 귀무가설을 채택할때는 '귀무가설 채택' 이 아니라 '귀무가설을 기각할 근거가 없다.' 라고 말한다. 기각하고 싶었는데 기각을 못했다. 라는 느낌으로..
지금 이 설명이 편견과 선입견이 난무하고 있는것같지만 애초에 이 가설검정 방법론이 세팅됐을때부터 나온 얘기여서 이 뉘앙스를 파악하는것이 굉장히 중요하다.
정리: 대립가설을 채택하지 않을 이유가 없다. 라는건 이건 무조건 채택을 해야만 했다. 할수밖에 없었다. 라는 강력한 근거를 말한거라고 이해하면 좋다!!
시각적 이해
아래 그래프는 이를 시각적으로 표현한 것이다:
- 중앙의 표준 정규 분포 곡선: 평균이 0인 종 모양의 곡선
- 임계값 위치: x축의 -1.96과 1.96에 수직선이 그려졌으며, 이 영역 외부는 기각 영역
- 계산된 z-값의 위치: x축의 2.74 위치에 수직선이 그려져 있으며, 이 선은 기각 영역 내에 있다.
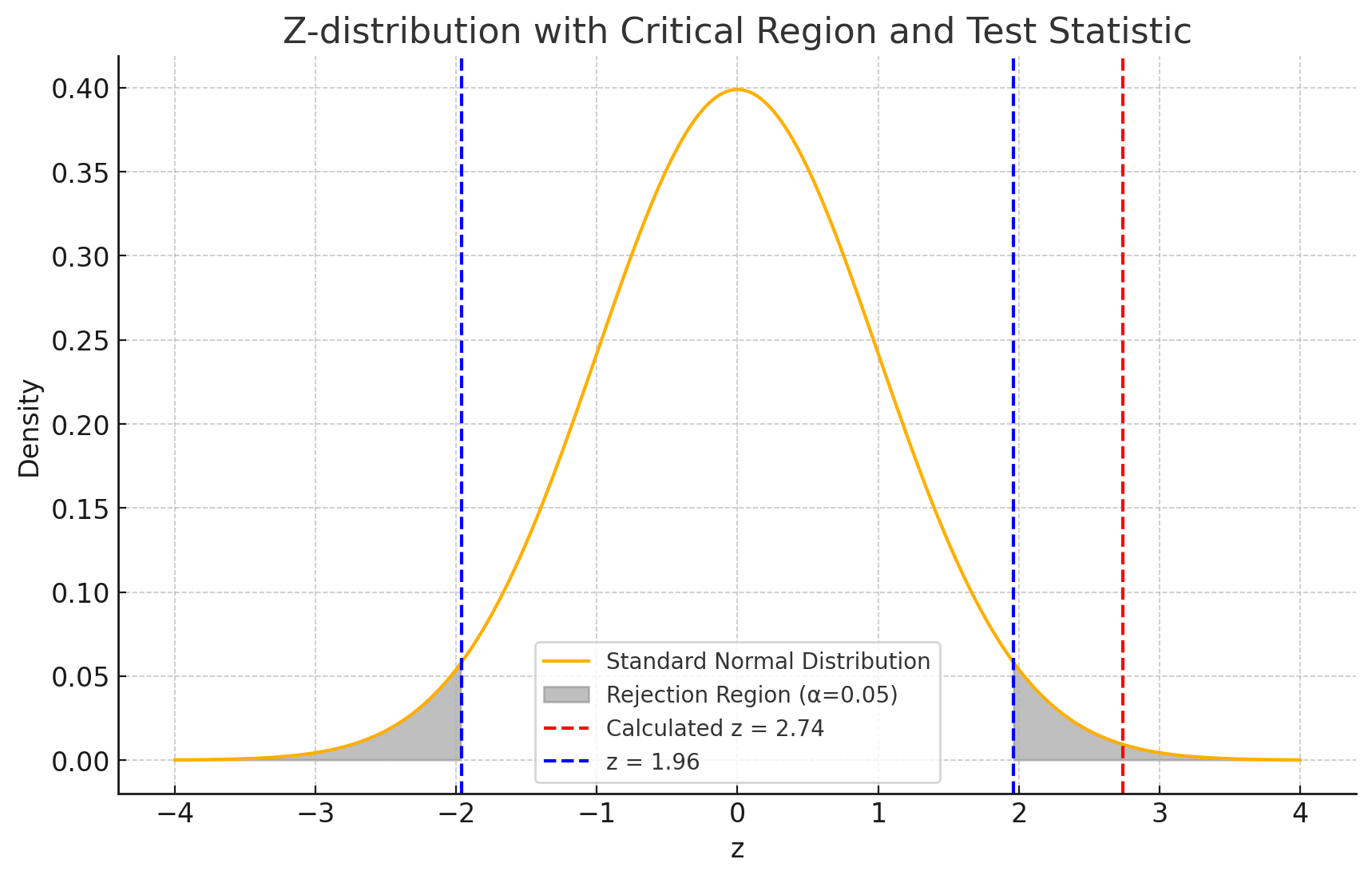
이 그래프를 통해 알 수 있듯이, 계산된 z-값이 기각 영역에 속하므로 우리는 귀무가설을 기각하고 대립가설을 채택하지 않을 이유가 없음을 보였줬다.
가설 검정에서는 데이터에 기반하여 귀무가설을 유지할지 기각할지를 결정한다. 이 과정에서 유의수준 α와 임계값을 사용하여 기각할지 말지 판단한다. 예시에서는 유의수준 0.05(5%)를 기준으로 z-값을 계산하여, 귀무가설을 기각하고 대립가설을 채택할 수 있음을 확인했다.
'Upstage AI Lab 4기' 카테고리의 다른 글
| [CV 경진대회] 데이터 증강 기법, ViT 모델 사용 (0) | 2024.11.04 |
|---|---|
| [Upstage AI Lab 4기] '아파트 실거래가 예측' 경진대회 Private Rank 3등 후기 (1) | 2024.09.17 |
| 집합의 크기 (Cardinality) (0) | 2024.08.22 |
| [팀프로젝트] 페르소나를 이용한 오은영 박사님 챗봇 (2) - chat history와 주제와 관계 없는 질문 회피 (1) | 2024.08.19 |
| [팀프로젝트] 페르소나를 이용한 오은영 박사님 챗봇 (1) 데이터 수집 및 임베딩, 쿼리 테스트 (0) | 2024.08.13 |

가설 검정
가설 검정은 통계적으로 어떤 주장(귀무가설)이 사실인지 확인하는 방법이다. 이 과정에서 우리는 두 가지 가설을 세 운다:
- 귀무가설 (H_0): 보통 우리가 검정하고자 하는 기본 가정. (마음속으로는 기각하고자 하는 가정)
- 대립가설 ((H_1)): 귀무가설이 사실이 아닐 경우를 나타내는 가설. (마음속으로는 채택하고 싶은 가정)
유의수준 (α)과 1종 오류
유의수준(α)은 가설 검정에서 귀무가설을 잘못 기각할 확률을 나타낸다. 이 값은 우리가 허용하는 1종 오류의 최대 확률이다. 1종 오류는 귀무가설이 사실임에도 불구하고 이를 기각하는 오류를 의미한다. 일반적으로 유의수준은 0.05(5%)로 설정되며, 이는 “귀무가설이 사실일 때 5%의 확률로 잘못된 결정(귀무가설 기각)을 내릴 수 있다”는 뜻 이다.

이때 유의수준이 중요한 이유는, 가설 검정의 목표가 대립가설을 검증하기 위함이라는 점에 있다. 즉, 귀무가설을 기각하고 대립가설을 채택하고자 하는 경향이 있으므로, 이 과정에서 발생할 수 있는 오류(1종 오류)를 가능한 한 최소화하고자 유의수준을 설정하는 것이다.
z-값 (z-score): 검정통계량
검정통계량(Test Statistic)은 가설 검정에서 우리가 어떤 결정을 내릴 때 사용하는 중요한 도구이다. 이를 통해 우리가 얻은 표본 데이터를 바탕으로 귀무가설을 기각할지 아니면 유지할지를 판단할 수 있다.
검정통계량은 주어진 표본 데이터를 바탕으로 계산된 통계량으로, 가설 검정에서 사용된다. 이를 통해 주어진 표본이 귀무가설 하에서 얼마나 벗어나 있는지를 평가할 수 있다. 검정통계량의 종류는 여러 가지가 있으며, 그 중 하나가 z-값이다.
z-값은 검정통계량 중 하나로, 주어진 데이터가 귀무가설 하에서 얼마나 벗어나 있는지를 측정하는 값이다. 이는 표본 평균이 귀무가설에서 가정된 모평균으로부터 몇 개의 표준 편차만큼 떨어져 있는지를 나타낸다. z-값이 크다면, 표본 평균이 귀무가설 하의 모평균으로부터 많이 떨어져 있다는 의미이며, 이 경우 귀무가설을 기각할 가능성이 크다. 반대로 z-값이 작다면, 표본 평균이 귀무가설 하의 모평균에 가깝다는 의미이며, 귀무가설을 기각하지 않을 가능성이 크다.
z-값은 다음과 같은 식으로 계산된다:
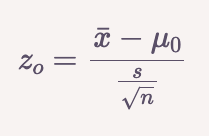
- bar(x): 표본 평균
- mu_0: 귀무가설 하에서의 모평균(가정된 평균)
- s: 표본 표준편차
- n: 표본 크기
즉, 검정통계량으로서 z-값을 사용하여, 우리가 얻은 표본이 귀무가설에서 가정된 평균으로부터 얼마나 벗어나 있는지를 평가하고, 이를 바탕으로 귀무가설을 기각할지 유지할지를 결정하는 것이다.
임계값과 기각역
- 기각역: 유의수준에 따라 검정통계량이 귀무가설을 기각할 수 있는 영역을 기각역이라고 한다. α = 0.05인 경우, 양측 검정에서는 기각역이 표준 정규 분포의 양쪽 끝 각각 2.5%씩에 해당한다. 이 기각역을 구체적으로 결정하기 위해 임계값(critical value)을 사용한다.
- 임계값: 임계값은 표준 정규 분포에서 유의수준에 대응하는 z-값이다. α = 0.05의 경우, 임계값은 ±1.96으로 설정된다. 즉, z-값이 1.96보다 크거나 -1.96보다 작다면, 이는 기각역에 속하게 되며 귀무가설을 기각할 수 있다.
예시로 보는 가설검정
예시는 단일 표본 t-test이다.
어느 제과 회사에서 나오는 쿠키의 평균 무게가 50g인지 확인하기 위해 30개의 샘플을 조사했다. 이 샘플들의 평균 무게는 52g이었고, 표준편차는 4g이었다. 이 정보를 바탕으로 z-값을 계산해 보니, 2.74가 나왔다.
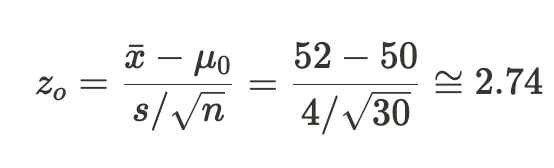
이제, 이 z-값을 임계값과 비교해보자. α = 0.05일 때, 임계값은 ±1.96이다. 계산된 z-값 2.74는 1.96을 초과하므로, 이 값은 기각역에 속한다.
즉, "쿠키의 평균 무게는 50g이다" 라는 귀무가설을 기각하고 "쿠키의 평균 무게는 50g이 아니다" 라는 대립가설을 채택하지 않을 이유가 없음을 보였다.
'대립가설을 채택했다.' 하고 하면 그냥 채택된것으로 끝난다.
'채택하지 않을 이유가 없음을 보였다.' 라는건 이건 빼박이다. 라는 소리다. 무조건 채택 해야해. 라는 뉘앙스다.
지금은 연습문제니까 그냥 '저 이거 채택했는데요?'라고 할 수 있지만 어디 학회에서 발표를 할때 근거를 얘기할때 '채택했다.' 이렇게 말하면 '너 대립가설 기각할수도 있었자나' 이런 반박이 안나올 수 있다. 이때, '채택하지 않을 이유가 없어. 라고 말하면 좋다. 꼭 채택해야만 했었어. 라는 뉘앙스로 전달하는게 좋다.
이게 위에서 언급한 '귀무가설은 기각하고 싶고, 대립가설을 채택하고싶다'는 마인드가 반영이 된거다.
그리고 귀무가설을 채택할때는 '귀무가설 채택' 이 아니라 '귀무가설을 기각할 근거가 없다.' 라고 말한다. 기각하고 싶었는데 기각을 못했다. 라는 느낌으로..
지금 이 설명이 편견과 선입견이 난무하고 있는것같지만 애초에 이 가설검정 방법론이 세팅됐을때부터 나온 얘기여서 이 뉘앙스를 파악하는것이 굉장히 중요하다.
정리: 대립가설을 채택하지 않을 이유가 없다. 라는건 이건 무조건 채택을 해야만 했다. 할수밖에 없었다. 라는 강력한 근거를 말한거라고 이해하면 좋다!!
시각적 이해
아래 그래프는 이를 시각적으로 표현한 것이다:
- 중앙의 표준 정규 분포 곡선: 평균이 0인 종 모양의 곡선
- 임계값 위치: x축의 -1.96과 1.96에 수직선이 그려졌으며, 이 영역 외부는 기각 영역
- 계산된 z-값의 위치: x축의 2.74 위치에 수직선이 그려져 있으며, 이 선은 기각 영역 내에 있다.

이 그래프를 통해 알 수 있듯이, 계산된 z-값이 기각 영역에 속하므로 우리는 귀무가설을 기각하고 대립가설을 채택하지 않을 이유가 없음을 보였줬다.
가설 검정에서는 데이터에 기반하여 귀무가설을 유지할지 기각할지를 결정한다. 이 과정에서 유의수준 α와 임계값을 사용하여 기각할지 말지 판단한다. 예시에서는 유의수준 0.05(5%)를 기준으로 z-값을 계산하여, 귀무가설을 기각하고 대립가설을 채택할 수 있음을 확인했다.
'Upstage AI Lab 4기' 카테고리의 다른 글
| [CV 경진대회] 데이터 증강 기법, ViT 모델 사용 (0) | 2024.11.04 |
|---|---|
| [Upstage AI Lab 4기] '아파트 실거래가 예측' 경진대회 Private Rank 3등 후기 (1) | 2024.09.17 |
| 집합의 크기 (Cardinality) (0) | 2024.08.22 |
| [팀프로젝트] 페르소나를 이용한 오은영 박사님 챗봇 (2) - chat history와 주제와 관계 없는 질문 회피 (1) | 2024.08.19 |
| [팀프로젝트] 페르소나를 이용한 오은영 박사님 챗봇 (1) 데이터 수집 및 임베딩, 쿼리 테스트 (0) | 2024.08.13 |
